C5 Timber Framing Angle

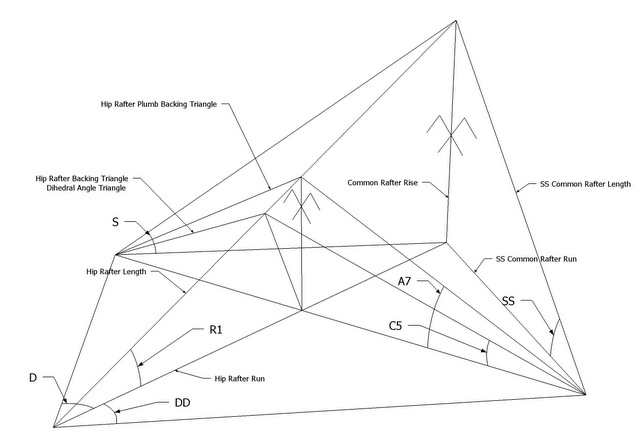
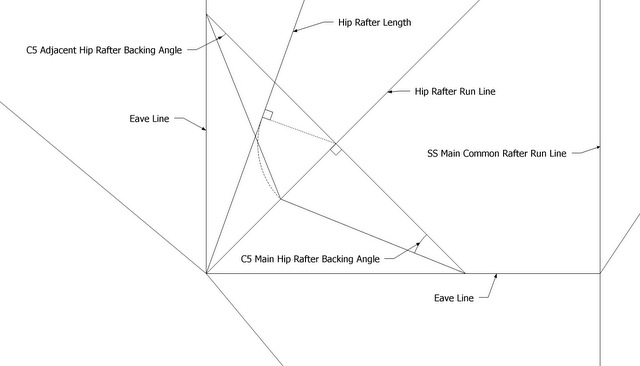
Timber Framing Angle: C5
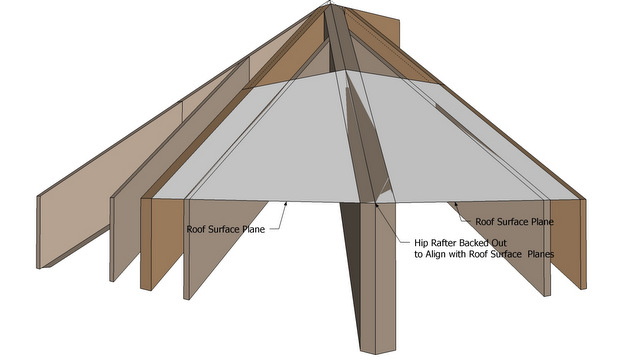
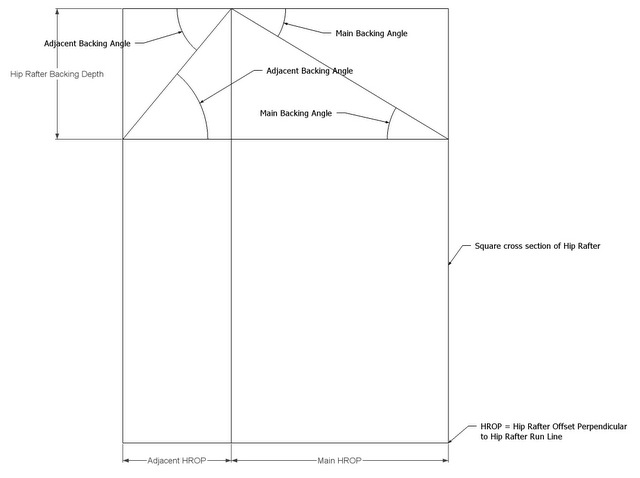
C5 = Hip Rafter Backing Angle, the Saw Blade Bevel Angle to cut an edge bevel on a Hip Rafter or trough on a Valley Rafter. Also the Saw Blade Bevel Angle when cutting along the Sheathing Angle, the angle on the face of the Purlin set in the plane of the roof (the Sheathing Angle) or the complementary Jack Rafter Side Cut Angle. This plane is perpendicular to the hip rafter slope line.

C5 = arctan (sin R1 ÷ tan D)

C5 = arccos (sin DD ÷ cos P2)
C5 = arccos (sin DD ÷ sin 90 - P2)
C5 = arccos (cos SS ÷ cos R1)
C5 = arcsin (sin SS x cos DD)
C5 = arctan (tan SS x sin P2)
C5 = arctan (tan SS x cos 90 - P2)
C5 = arcsin (tan P2 x tan R1)
C5 = arcsin (tan R1 ÷ tan 90 - P2)
C5 = arctan (sin R1 ÷ tan DD)
C5 = arctan (sin R1 x tan D)

C5 = arccos (sin Plan Angle ÷ cos Jack Rafter Side Cut Angle)
C5 = arccos (sin Plan Angle ÷ sin Sheathing Angle)
C5 = arccos (cos Common Rafter Pitch Angle ÷ cos Hip-Valley Pitch Angle)
C5 = arcsin (sin Common Rafter Pitch Angle x cos Plan Angle)
C5 = arctan (tan Common Rafter Pitch Angle x sin Jack Rafter Side Cut Angle)
C5 = arctan (tan Common Rafter Pitch Angle x cos Sheathing Angle)
C5 = arcsin (tan Jack Rafter Side Cut Angle x tan Hip-Valley Pitch Angle)
C5 = arcsin (tan Hip-Valley Pitch Angle ÷ tan Sheathing Angle)
C5 = arctan (sin Hip-Valley Pitch Angle ÷ tan Plan Angle)
C5 = arctan (sin Hip-Valley Pitch Angle x tan Adjacent Plan Angle)
Hip Rafter Backing Angle = arctan( sin( Hip Rafter Pitch Angle) ÷ tan( Plan Angle ) )

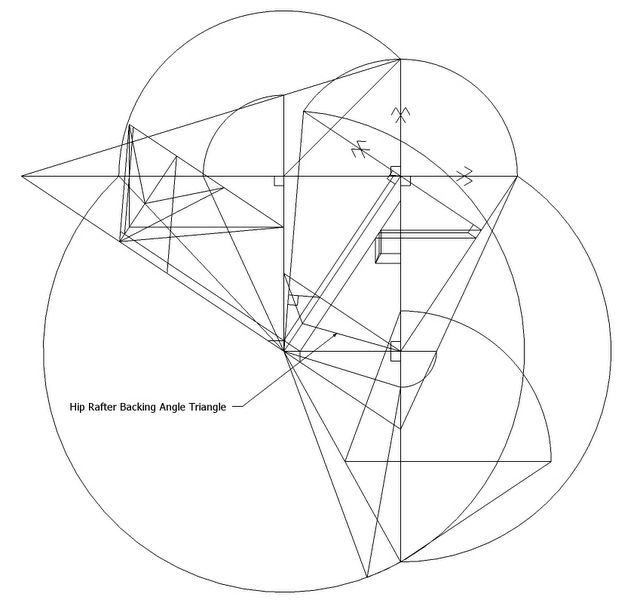
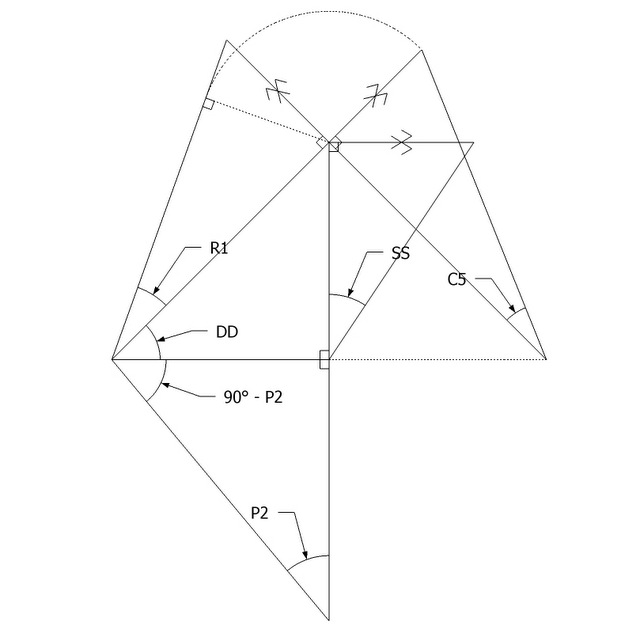
The Hip-Valley Roof Ratios Angle Formulas were developed by Joe Bartok.

The Timber Framing Hawkindale Angle Formulas were developed by Rees Hawkins Acheson from the Martindale Hip and Valley Roof Angles and Hawkindale angle drawings by Ed Levin of the Timber Framers Guild.

The Hawkindale angles were based on the book by Frank L. Martindale "Bevel Angles for Three Dimensional Connections" 1948 that was based on the book "Hip and Valley Design" by H. L. McKibben and L. E. Gray published in 1912.